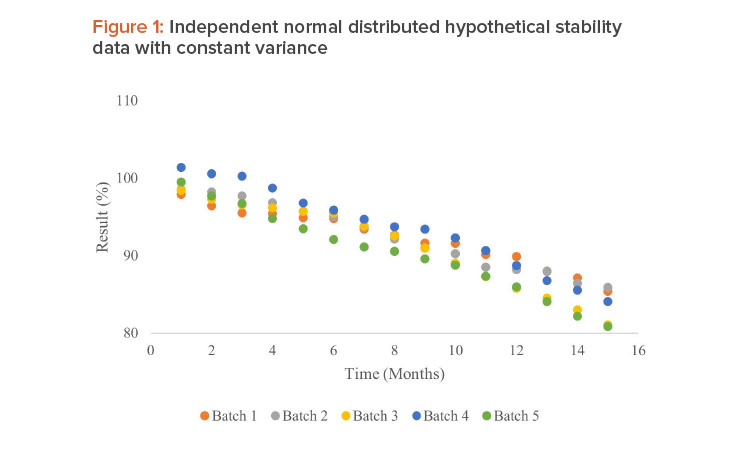
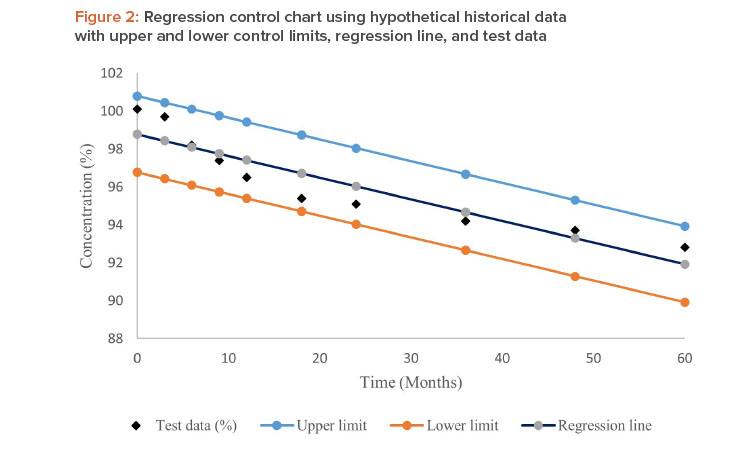
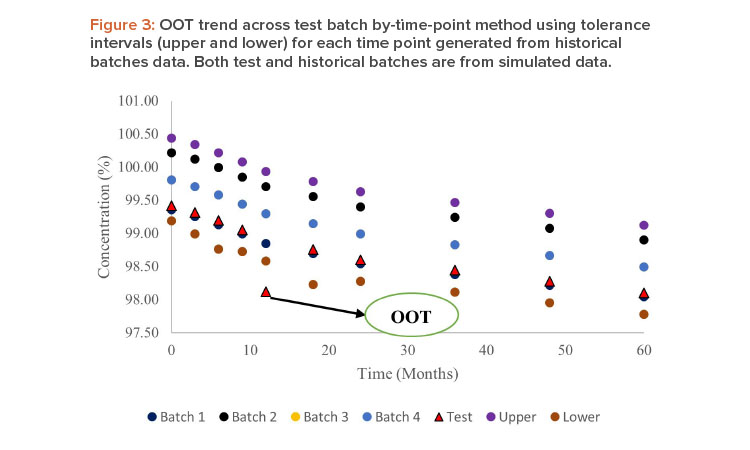
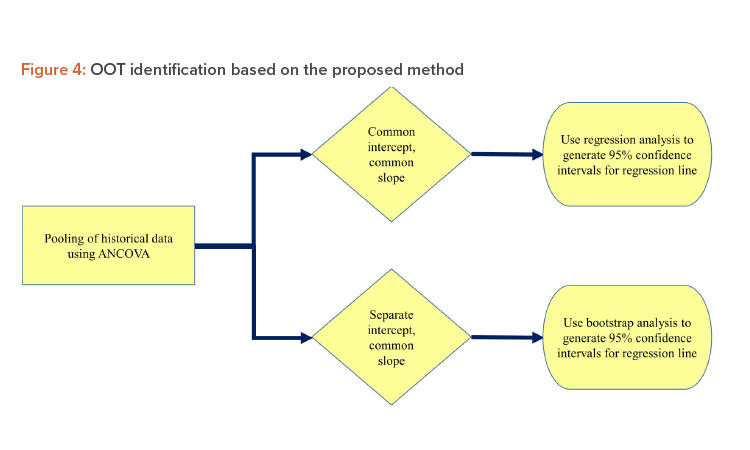
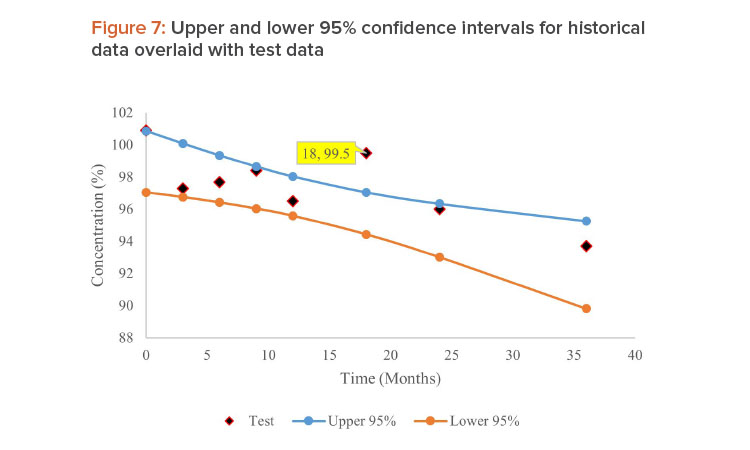
The goal of this article is to create a new method to identify OOT based on the regression control chart method. In the first step, data from all the historical batches are tested for pooling using analysis of covariance (ANCOVA). If the historical batches can be pooled using the common intercept and common slope (CICS) model, then regression analysis of data from historical batches is performed and the 95% confidence intervals (CI) for the regression line are obtained. If any data points from the test batch fall outside the 95% CI limit, the data are considered OOT.
If the historical batches can be pooled using the separate intercept and common slope (SICS) model, bootstrap analysis is performed on the historical data to generate 95% CI for the regression line. If any data points from the test batch fall outside the 95% CI limit, they are examined as OOT. This method cannot be applied if the data from historical batches cannot be pooled: In this case, the separate intercept and separate slope (SISS) model would be used for ANCOVA analysis. The schematic outline of this method is shown in Figure 4.
The 95% CI, for the dependent variable (yi) for a given independent variable (xi), is given by the following equation :
$$\begin{align} (mx_i + b) \pm t(\alpha, n - 2) \times S_{yx} \times \sqrt{\frac{1}{n} + \frac{(x_i - \bar{x})^2}{\sum_{i=1}^n (x_i - \bar{x})^2}} \tag{2} \end{align} $$
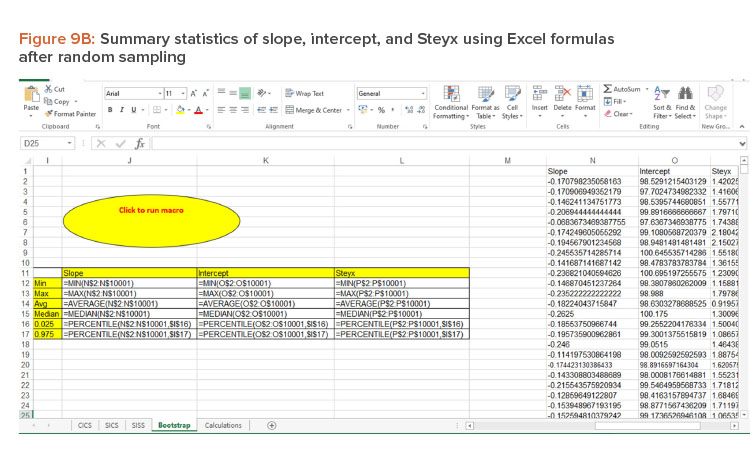
Where m equals slope, b equals intercept, a equals significance level (0.05), n equals number of observations, and Syx equals the standard error of the predicted y value for each x in the regression. It is a measure of the amount of error in the prediction of y for an individual x. This value can be obtained by STEYX function in Microsoft Excel .
ANCOVA
A covariate is a variable that is not the variable of research interest, but may affect the dependent variable and its relationship with the independent variable. The effect of a covariate variable is controlled by changing the variance of dependent variables. It is also controlled by the relationship between the dependent variable and the covariate at different levels of variables being analysed.
ANCOVA analysis is a statistical method that involves combination of analysis of variance (ANOVA) and regression analysis for adjusting the linear effect of covariate. The main advantage of using ANCOVA is its ability to uncover variance changes of the dependent variable due to change in the covariate and to discriminate it from the changes in variance due to changes in the levels of the qualitative variable. ANCOVA reduces errors in dependent variables and increases analytical power .
Materials and Methods
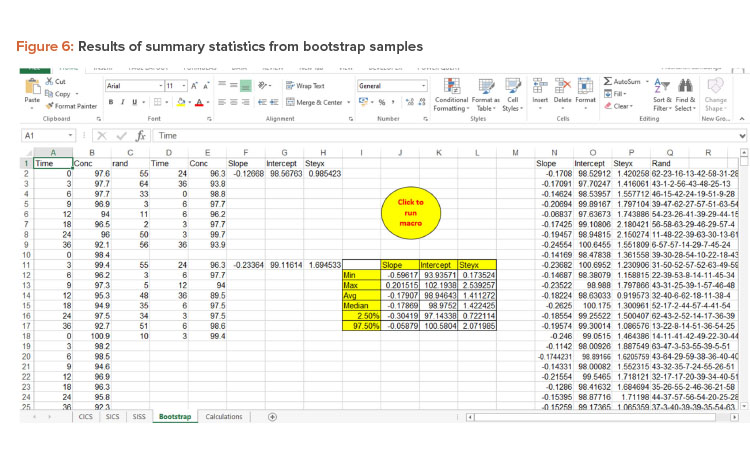
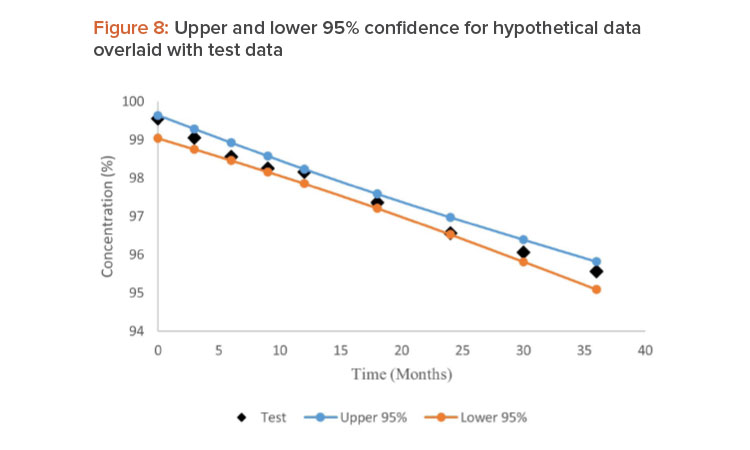
Data in Table 1 reported by Mihalovits and Sándor containing eight batches of historical data and the ninth batch as test data were used to demonstrate this approach . The historical data were tested for pooling criteria using ANCOVA method in Microsoft Excel. Based on the model used for pooling historical data, 95% CIs for the regression line were obtained. Hypothetical data in Table 2 containing three historical batches and one test batch were used.
Data Pooling Using ANCOVA
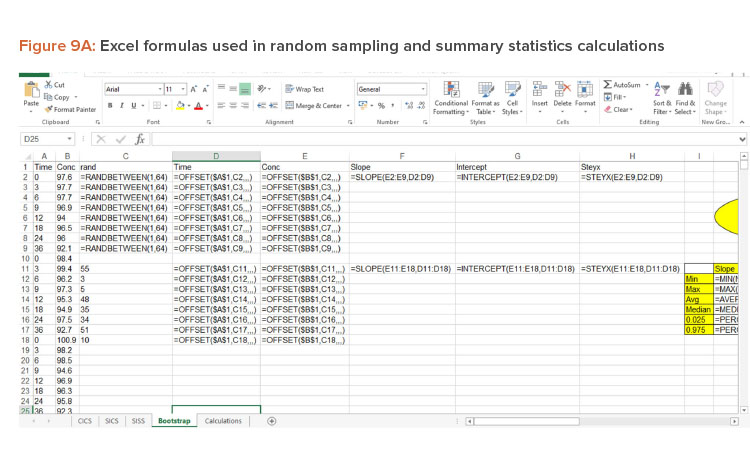
The use of Microsoft Excel to test the equality of slopes and intercepts using ANCOVA for three batches was described by LeBlond . When the number of test batches is greater than three, the test for equality of slope and intercepts using Microsoft Excel was described by Sambaraju . In these tests, a significance level of 0.05 was used as the criterion for pooling. Based on ANCOVA analysis results, the SICS model was used to pool the data from historical batches.
Bootstrap Method
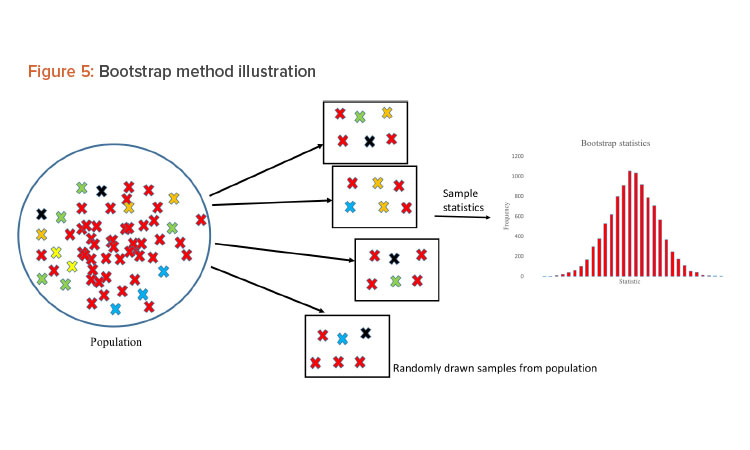
The bootstrap method was employed to generate 95% CIs for the regression line. The bootstrap method was introduced by Efron in 1979 to assess the statistical accuracy of the estimator . It is a computer-based resampling technique that uses new samples with repetition from original sample data to estimate the relevant properties of the population.